常见排序算法

发表于 | 分类于 ， |

​ 本文对比较常用且比较高效的排序算法进行了总结和解析，并贴出了比较精简的实现代码。

常见排序算法比较

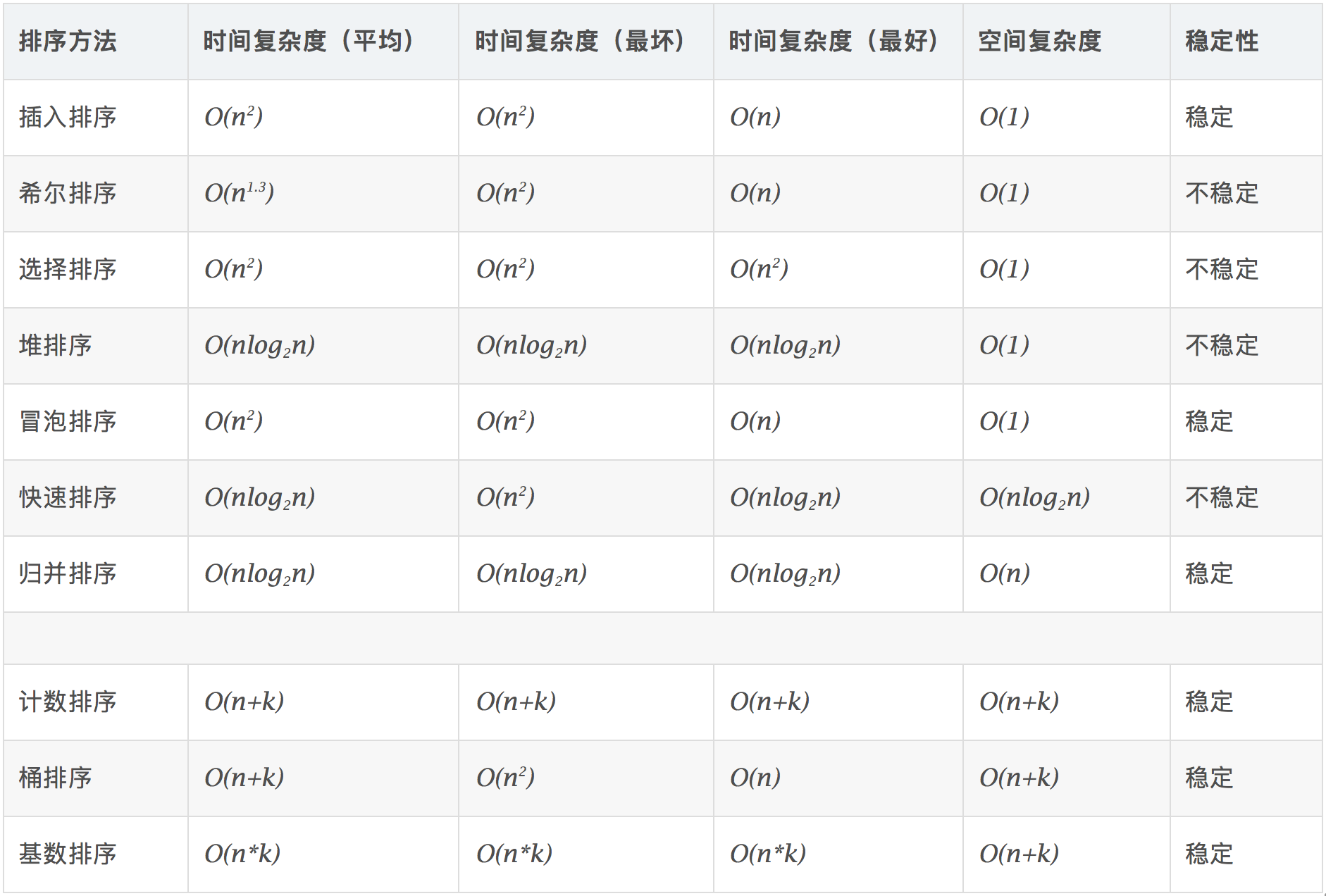
常见排序算法比较

相关概念

  • 稳定: 如果a原本在b前面，而a=b,排序之后a仍然在b的前面。
  • 不稳定: 如果a原本在b的前面，而a=b, 排之后a可能会出现在b的后面。
  • 时间复杂度: 对排序数据的总的操作次数。反映当n变化时，操作次数呈现什么规律。
  • 空间复杂度: 是指算法在计算机内执行时所需存储空间的度量，它也是数据规模n的函数。

冒泡排序

基本思想：从无序序列头部开始，进行两两比较，根据大小交换位置，直到最后将最大（小）的数据元素交换到了无序队列的队尾，从而成为有序序列的一部分；下一次继续这个过程，直到所有数据元素都排好序。

1
2
3
4
5
6
7
8
9
10
11
// 冒泡排序 
void bubble_sort(int a[], int n) {
    for(int i=0; i<n-1; i++)
    {
        for(int j=0; j<n-i-1; j++)
        {
            if(a[j]>a[j+1])
                swap(a[j], a[j+1]);   //交换数据
        }
    }
}

快速排序

基本思想：基于分治法。在待排序表L[1…n]中任取一个元素pivot作为基准，通过一趟排序算法将待排序表划分为独立的两部分L[1…k-1]和L[k+1…n]，使得L[1…k-1]中的所有元素小于pivot，L[k+1…n]中的所有元素大于等于pivot，则pivot放在了其最终位置L[k]上，这个过程称为一趟快速排序。而后分别递归地对两个子表重复上述过程，直至每部分内只有一个元素或空为止，即所有元素都放在了其最终位置上。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
void QuickSort(int a[], int low, int high) //快排母函数
 {
   if(low < high){
     int pivot = Paritition(a, low, high);
     QuickSort(a, low, pivot - 1);
     QuickSort(a, pivot + 1, high);
   }
 }

//严蔚敏《数据结构》标准分割函数
int Paritition(int a[], int low, int high) {
    int pivot = a[low];   // 第一个元素设为枢轴，对表进行划分
    while(low < high) {
         while(low<high && a[high]>=pivot) --high;
         a[low] = a[high];  // 将比枢轴小的元素移动到左端
         while (low<high && a[low]<=pivot) ++low;
         a[high] = a[low];  // 将比枢轴大的元素移动到右端
    }
    a[low] = pivot;     // 枢轴元素存放到最终位置
    return low;        // 返回最终位置
 }
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
//快排优化思想：主要是关于基准pivot的选择
//三种选法：固定选取，随机选取，三数取中法

//随机选取
void QuickSort_Random(int a[], int low, int high) //快排母函数
 {
   if(low < high){
     int pivot = Parition_Random(a, low, high);
     QuickSort_Random(a, low, pivot - 1);
     QuickSort_Random(a, pivot + 1, high);
   }
 }

//随机选取，随机划分操作，随机选pivot
int Parition_Random(int a[], int low, int high){
    int i = rand()%(high-low)+low;
    swap(a[low], a[i]);
    return Parition(a, low, high);
}

//严蔚敏《数据结构》标准分割函数
int Parition(int a[], int low, int high) {
    int pivot = a[low];   // 第一个元素设为枢轴，对表进行划分
    while(low < high) {
         while(low<high && a[high]>=pivot) --high;
         a[low] = a[high];  // 将比枢轴小的元素移动到左端
         while (low<high && a[low]<=pivot) ++low;
         a[high] = a[low];  // 将比枢轴大的元素移动到右端
    }
    a[low] = pivot;     // 枢轴元素存放到最终位置
    return low;        // 返回最终位置
 }
1
2
3
4
5
6
7
8
9
10
11
12
13
//三数取中的思想：选取数组开头，中间和结尾的元素，通过比较选中间的值作为快排的划分点
int selectMedianofThree(int a, int b, int c){ //三数取中
    if((a-b)*(a-c)<=0) return a;
    if((b-a)*(b-c)<=0) return b;
    if((c-a)*(c-b)<=0) return c;
}

int Parition(int a, int low, int high){
    int pivot=selectMedianofThree(a[low], a[(low+high)/2], a[high]);
    while(low<high){
        //然后和第一种一样
    }
}

直接插入排序

基本思想： 将数组中的所有元素依次和前面的已经排好序的元素相比较（依次），如果选择的元素比已排序的元素小，则交换，直到全部元素都比较过。

1
2
3
4
5
6
7
8
9
10
11
12
13
void insert_sort(int a[],int n) {
    //外层循环标识并决定待比较的数值
    for(int i=1; i < n; i++) {           //循环从第2个元素开始
        if(a[i] < a[i-1]) {
            int temp = a[i];
            //待比较数值确定其最终位置
            for(int j = i-1; j >= 0 && a[j] > temp; j--) {
                a[j+1] = a[j];  //移动
            }
            a[j+1] = temp;           //此处就是a[j+1]=temp;
        }
    }
}

希尔排序

基本思想：希尔排序也称缩小增量排序；希尔排序是把记录按下标的一定增量分组，对每组使用直接插入排序算法排序，随着增量逐渐减少，每组包含的关键词越来越多，当增量减至1时（用gap = gap/3+1 控制），保证了最后一次进行直接插入排序，算法终止。

1
2
3
4
5
6
7
8
9
10
11
12
void shell_sort(int a[], int n) {
    int gap;
	while (gap < n / 3)
		gap = gap * 3 + 1; 
	for (; gap > 0; gap /= 3)
		for (int i = gap; i < n; i++) {
			int temp = a[i];
			for (int j = i - gap; j >= 0 && a[j] > temp; j -= gap)
				a[j + gap] = a[j];  //移动
			a[j + gap] = temp;
		}
}

简单选择排序

基本思想：首先在未排序序列中找到最小（大）元素，存放到排序序列的起始位置。再从剩余未排序元素中继续寻找最小（大）元素，然后放到已排序序列的末尾。重复第二步，直到所有元素均排序完毕。

1
2
3
4
5
6
7
8
9
void select_sort(int a[],int n)
{
    for(int i = 0; i < n-1; ++i)
    {
        for(int j = i+1; j < n; ++j)
            if(a[j] < a[i])
                swap(a[i], a[j]);
    }
}

堆排序

堆

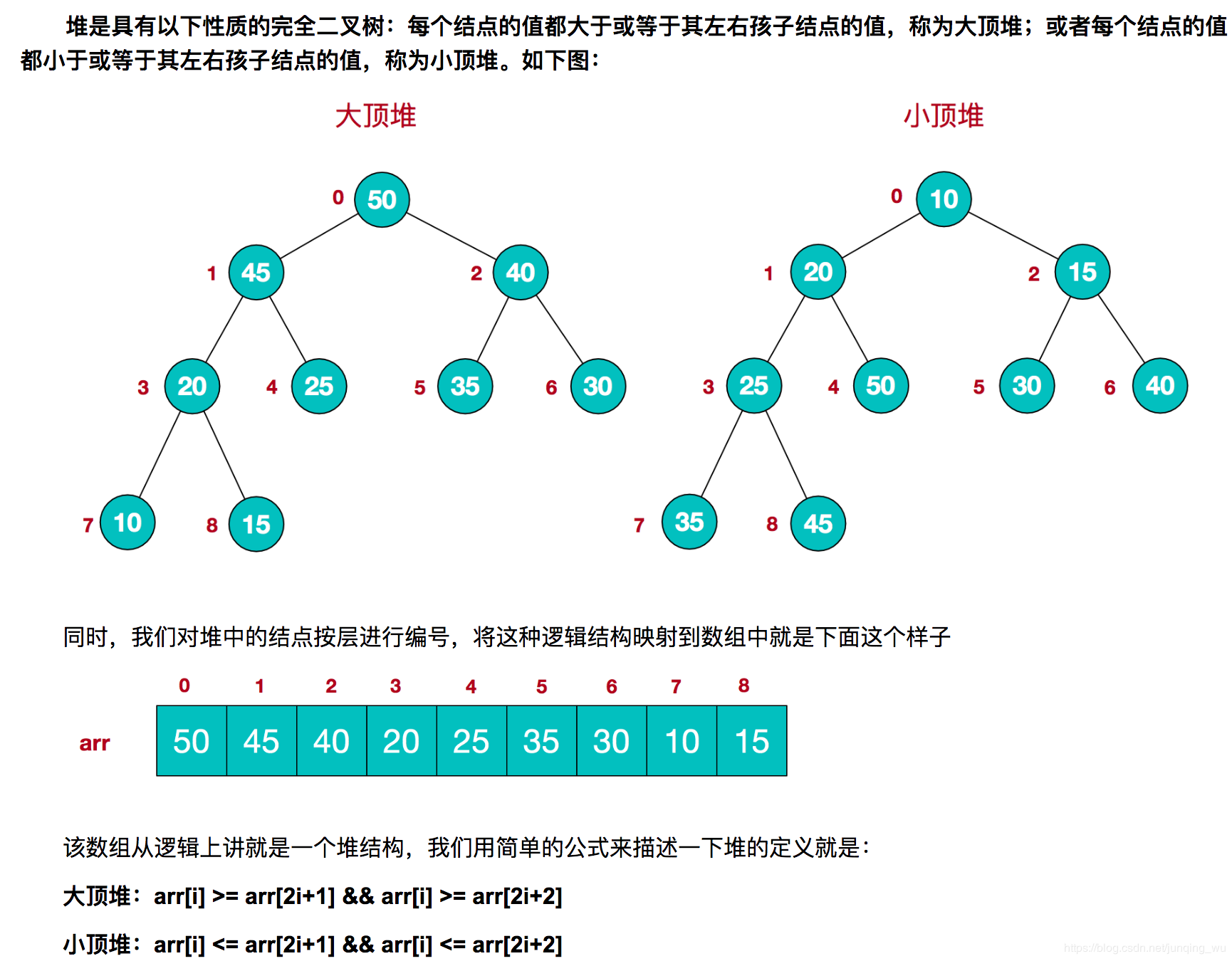
基本思想：将待排序序列构造成一个大顶堆，此时，整个序列的最大值就是堆顶的根节点。将其与末尾元素进行交换，此时末尾就为最大值。然后将剩余n-1个元素重新构造成一个堆，这样会得到n个元素的次小值。如此反复执行，便能得到一个有序序列了。

  1. 步骤一 构造初始堆。将给定无序序列构造成一个大顶堆（一般升序采用大顶堆，降序采用小顶堆)。
  2. 此时我们从最后一个非叶子结点开始（叶结点自然不用调整，第一个非叶子结点 为 倒数第二层左右边的节点），从左至右，从下至上进行调整。
  3. 将堆顶元素与末尾元素进行交换，使末尾元素最大。然后将剩余的n-1个元素继续调整堆(只需调整堆顶元素)，再将堆顶元素与末尾元素交换，得到第二大元素。如此反复进行交换、重建、交换。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
// 堆排序的核心是建堆，传入参数为数组，数组长度
void BuildMaxHeap(int a[], int len){ // 建立大根堆
    for(int i=len/2; i>0; i--){   // 从最后一个非叶子节点的父结点开始建堆
        AdjustDown(a, i, len);
    }
}
// 堆向下调整算法，传入参数为数组，根节点位置，数组长度
void AdjustDown(int a[], int k, int len) {
    a[0] = a[k];
    for(int i = 2*k; i <= len; i *= 2) {  // 沿k较大的子节点向下筛选
        if(i<len && a[i]<a[i+1])
            i++;                          // 取k较大的子节点的下标
        if(a[0]>=a[i]) break;       // 筛选结束
        else {
            a[k] = a[i];            // 将nums[i]调整到双亲节点上
            k = i;                        // 修改k值，以便继续向下筛选
        }
    }
    a[k] = a[0]                     // 被筛选节点的值放入最终位置
}
// 堆排序算法
void Heap_sort(int a[], int len) {
    BuildMaxHeap(a, len);              // 初始建堆
    for(i=len; i > 1; i--) {            
        swap(a[i], a[1]);           // 输出堆顶元素（和堆底元素交换）
        AdjustDown(a, 1, i-1);         // 调整，把剩下的i-1个元素调整成堆
    } 
}
// 堆向上调整算法
void AdjustUp(int nums[], int k) {
// 参数k为向上调整的节点，也为堆的元素个数
    nums[0] = nums[k];
    int i = k/2;
    while(i>0 && nums[i]<nums[0]) {
        nums[k] = nums[i];
        k = i;
        i = i/2;
    }
    nums[k] = nums[0];
}

归并排序

基本思想：归并排序是建立在归并操作上的一种有效的排序算法。该算法是采用分治法(Divide and Conquer)的一个非常典型的应用。将已有序的子序列合并，得到完全有序的序列; 即先使每个子序列有序，再使子序列段间有序。若将两个有序表合并成一个有序表，称为2-路归并。

2-路归并：

  • 分解：将含有n个元素的待排序表分成含n/2个元素的子表，采用2路归并排序算法对两个子表递归地进行排序。
  • 合并：合并两个已经排序的子表得到排序结果。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
void MergeSort(vector<int>& nums, int low, int high){
    if(low>=high){  //终止递归的条件，子序列长度为1
        return ;
    }
    int mid=low+(high-low)/2;     //取得序列中间的元素
    MergeSort(nums, low, mid);    //对左半边递归
    MergeSort(nums, mid+1, high); //对右半边递归
    Merge(nums, low, mid, high);  //合并
}
//合并两个已排序的子表
void Merge(vector<int>& nums, int low, int mid, int high){
    vector<int> temp(nums.size());  //辅助数组
    for(int i=low;i<=high;i++){     //将nums复制到辅助数组
        temp[i]=nums[i];            //以便合并后的结果能够直接存入到nums中
    }
    //数组双指针技巧，合并两个有序数组
    //low为第1有序区的第1个元素，i指向第1个元素, mid为第1有序区的最后1个元素
    int i=low, j=mid+1;  // mid+1为第2有序区第1个元素，j指向第1个元素
    for(int k=low;k<=high;k++){
        if(i==mid+1){
            //左半边数组已全部被合并
            nums[k] = temp[j++];
        }else if(j==high+1){
             //右半边数组已全部被合并
            nums[k] = temp[i++];
        }else if(temp[i]>temp[j]){
            nums[k] = temp[j++];
        }else{
            nums[k] = temp[i++];
        }
    }
}
-------------本文结束 感谢阅读-------------
0%