常见二叉树解题集合

二叉树思维篇：填充节点的右侧指针、二叉树展开为链表、树的子结构

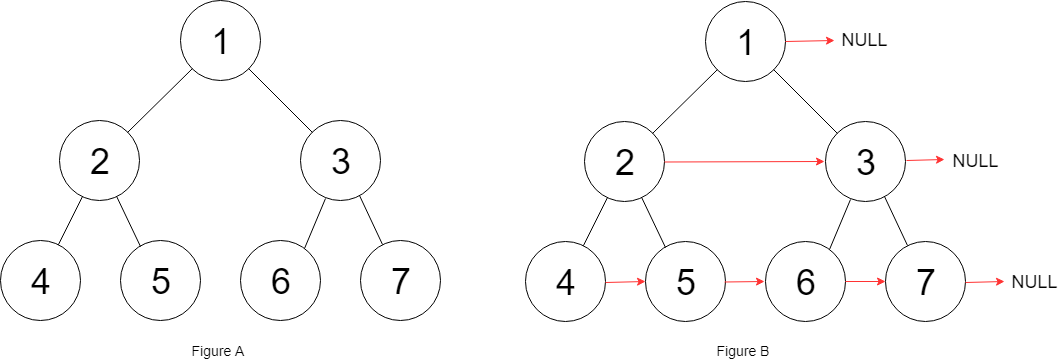
116.填充节点的右侧指针

/*
// Definition for a Node.
class Node {
public:
    int val;
    Node* left;
    Node* right;
    Node* next;
    Node() : val(0), left(NULL), right(NULL), next(NULL) {}
    Node(int _val) : val(_val), left(NULL), right(NULL), next(NULL) {}
    Node(int _val, Node* _left, Node* _right, Node* _next)
        : val(_val), left(_left), right(_right), next(_next) {}
};
*/
class Solution {
public:
    Node* connect(Node* root) {
        if(root==NULL) return NULL;
        traverse(root->left, root->right);
        return root;
    }
    void traverse(Node* node1, Node* node2){
        if(node1==NULL || node2==NULL){
            return ;
        }
        //前序遍历位置
        //将传入的两个节点连起来
        node1->next=node2;

        //连接相同父节点的两个字节点
        traverse(node1->left, node1->right);
        traverse(node2->left, node2->right);
        //连接跨越父节点的两个子节点
        traverse(node1->right, node2->left);
    }
};

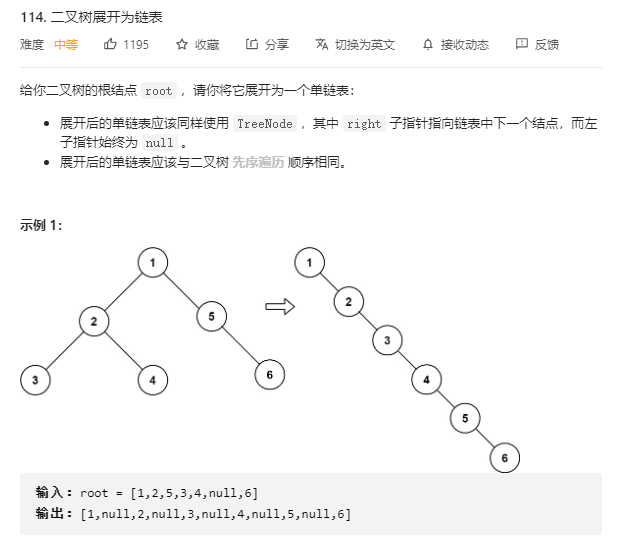
114.二叉树展开为链表

class Solution {
public:
    void flatten(TreeNode* root) {
        //递归实现，先将root的左右子树开展成单链表，再将右子树接到左子树
        //然后将整个左子树作为原树的右子树

        //base case
        if(root == nullptr) return ;
        
        //将左右子树拉平
        flatten(root->left);
        flatten(root->right);

        /***后序遍历位置***/
        //用两个临时节点来存左右子树
        TreeNode* left = root->left;
        TreeNode* right = root->right;

        //将左子树接过去
        root->left = nullptr;
        root->right = left;

        TreeNode* p = root;
        while(p->right){
            p = p->right;
        }
        p->right = right;
    }
};

offer I 二叉搜索树与双向链表

输入一棵二叉搜索树，将该二叉搜索树转换成一个排序的循环双向链表。要求不能创建任何新的节点，只能调整树中节点指针的指向。

思路：

定义两个指针pre和head，pre指针用于保存中序遍历的前一个节点，head指针用于记录排序链表的头节点。

中序遍历二叉树，遍历顺序就是双线链表的建立顺序。只需要在中序遍历的过程中，修改每个节点的左右指针，将零散的节点连接成双向循环链表。

/* // Definition for a Node.
class Node {
public:
    int val;
    Node* left;
    Node* right;
    Node() {}
    Node(int _val) {
        val = _val;
        left = NULL;
        right = NULL;
    }
    Node(int _val, Node* _left, Node* _right) {
        val = _val;
        left = _left;
        right = _right;
    }
};*/
class Solution {
public:
    Node* pre=NULL; //用于保存中序遍历的前一个节点
    Node* head=NULL; //用于记录排序链表的头节点
    Node* treeToDoublyList(Node* root) {
        if(root==NULL) return root;
        dfs(root);
        
        //连接首尾
        head->left = pre;
        pre->right = head;
        
        return head;
    }
    void dfs(Node* root){
        //base case
        if(root==NULL) return;
        //左子树
        dfs(root->left);

        /*中序遍历位置*/
        if(pre!=NULL) pre->right = root; //将前驱节点的右指针指向当前根节点
        else head = root; //保存链表头节点
        root->left = pre; //root的left指针指向其前驱
        pre = root; //前驱节点右移
        
        //右子树
        dfs(root->right);
    }
};

offer 26.树的子结构

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    bool isSubStructure(TreeNode* A, TreeNode* B) {
        //先序遍历树 A 中的每个节点 n_A ; (对应函数 isSubStructure(A, B) )
        //判断树 A 中 以 n_A 为根节点的子树是否包含树 B ; (对应函数 helper(A, B) )

        if(A==NULL || B==NULL) return false;
        return helper(A, B) || isSubStructure(A->left, B) || isSubStructure(A->right, B);
    }
    bool helper(TreeNode* A, TreeNode* B){
        if(B==NULL) return true;
        if(A==NULL) return false;
        if(A->val!=B->val) return false;
        return helper(A->left, B->left) && helper(A->right, B->right);
    }
};

572.另一棵树的子树

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    bool isSubtree(TreeNode* root, TreeNode* subRoot) {
        if(root==nullptr) return false;

        return isSame(root, subRoot) || isSubtree(root->left, subRoot) 
               || isSubtree(root->right, subRoot);
    }
    bool isSame(TreeNode* a, TreeNode* b){
        if(a==nullptr && b==nullptr) return true;
        if(a==nullptr || b==nullptr) return false;
        if(a->val!=b->val) return false;

        return isSame(a->left, b->left) && isSame(a->right, b->right);
    }
};

236.二叉树的最近公共祖先

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
        //后序遍历
        
        //base case
        if(root==NULL) return NULL;
        if(root==p || root==q) return root;

        TreeNode* left=lowestCommonAncestor(root->left, p, q);
        TreeNode* right=lowestCommonAncestor(root->right, p, q);

        if(left!=NULL && right!=NULL) return root;

        if(left==NULL && right==NULL) return NULL;

        return left==NULL ? right : left;
    }
};

class Solution {
public:
    int lowestCommonAncestor(TreeNode* root, int o1, int o2) {
        // 后序遍历
        
        //base case
        if(root==nullptr) return 0;
        if(root->val==o1 || root->val==o2) return root->val;
        
        int val1 = lowestCommonAncestor(root->left, o1, o2);
        int val2 = lowestCommonAncestor(root->right, o1, o2);
        
        if(val1!=0 && val2!=0) return root->val;
        
        if(val1==0 && val2==0) return 0;
        
        return val1==0 ? val2 : val1;
    }
};

判断是不是完全二叉树

class Solution {
public:
    bool isCompleteTree(TreeNode* root) {
        // write code here
        //空树一定是完全二叉树
        if(root==nullptr) return true;
        queue<TreeNode*> q;
        q.push(root);
        //定义一个首次出现的标记位
        bool flag = false;
        
        while(!q.empty()){
            int n=q.size();
            for(int i=0;i<n;i++){
                TreeNode* cur = q.front();
                q.pop();
                //标记第一次遇到空节点
                if(cur==nullptr){
                    flag = true;
                }else{
                    //后续访问已经遇到空节点了，说明经过了叶子
                    if(flag) return false;
                    q.push(cur->left);
                    q.push(cur->right);
                }
            }
        }
        return true;
    }
};

958. 二叉树的完全性检验

class Solution {
public:
    bool isCompleteTree(TreeNode* root) {
        //广度优先遍历

        //空树一定是完全二叉树
        if(root==nullptr) return true;
        queue<TreeNode*> q;
        q.push(root);
        //定义一个首次出现的标记位
        bool flag = false;

        while(!q.empty()){
            int n=q.size();
            for(int i=0;i<n;i++){
                TreeNode* cur = q.front();
                q.pop();
                //标记第一次遇到空节点
                if(cur==nullptr){
                    flag=true;
                }else{
                    //后续节点遇到空节点了，说明经过了叶子节点
                    if(flag) return false;
                    q.push(cur->left);
                    q.push(cur->right);
                }
            }
        }
        return true;
    }
};

判断是不是平衡二叉树

class Solution {
public:
    bool IsBalanced_Solution(TreeNode* pRoot) {
        if(pRoot==nullptr) return true;
        if(abs(maxDepth(pRoot->left)-maxDepth(pRoot->right))>1) return false;
        return IsBalanced_Solution(pRoot->left) && IsBalanced_Solution(pRoot->right);
    }
    int maxDepth(TreeNode* root){
        if(root==nullptr) return 0;
        return max(maxDepth(root->left), maxDepth(root->right))+1;
    }
};

863. 二叉树中所有距离为 K 的结点

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */

// 思路： unordered_map + dfs
class Solution {
public:
    vector<int> res;
    unordered_map<int, TreeNode*> mp;
    vector<int> distanceK(TreeNode* root, TreeNode* target, int k) {
        //从根节点出发，dfs，记录每个节点的父节点
        findParent(root);

        //从target出发，寻找深度为k的节点
        dfs(target, NULL, 0, k);
        return res;
    }

    void findParent(TreeNode* root){
        if(root->left!=NULL){
            mp[root->left->val]=root;
            findParent(root->left);
        }
        if(root->right!=NULL){
            mp[root->right->val]=root;
            findParent(root->right);
        }
    }

    void dfs(TreeNode* root, TreeNode* parent, int depth, int k){
        if(root==NULL){
            return;
        }
        if(depth==k){
            res.push_back(root->val);
            return;
        }
        if(root->left!=parent){
            dfs(root->left, root, depth+1, k);
        }
        if(root->right!=parent){
            dfs(root->right, root, depth+1, k);
        }
        if(mp[root->val]!=parent){
            dfs(mp[root->val], root, depth+1, k);
        }
    }
};